https://www.acmicpc.net/problem/2580
2580번: 스도쿠
스도쿠는 18세기 스위스 수학자가 만든 '라틴 사각형'이랑 퍼즐에서 유래한 것으로 현재 많은 인기를 누리고 있다. 이 게임은 아래 그림과 같이 가로, 세로 각각 9개씩 총 81개의 작은 칸으로 이루
www.acmicpc.net
문제
스도쿠는 18세기 스위스 수학자가 만든 '라틴 사각형'이랑 퍼즐에서 유래한 것으로 현재 많은 인기를 누리고 있다.
이 게임은 아래 그림과 같이 가로, 세로 각각 9개씩 총 81개의 작은 칸으로 이루어진 정사각형 판 위에서 이뤄지는데,
게임 시작 전 일부 칸에는 1부터 9까지의 숫자 중 하나가 쓰여 있다.
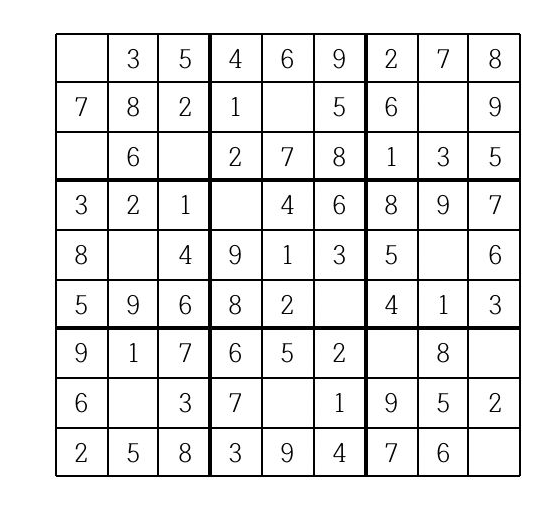
나머지 빈 칸을 채우는 방식은 다음과 같다.
- 각각의 가로줄과 세로줄에는 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.
- 굵은 선으로 구분되어 있는 3x3 정사각형 안에도 1부터 9까지의 숫자가 한 번씩만 나타나야 한다.
위의 예의 경우, 첫째 줄에는 1을 제외한 나머지 2부터 9까지의 숫자들이 이미 나타나 있으므로 첫째 줄 빈칸에는 1이 들어가야 한다.

또한 위쪽 가운데 위치한 3x3 정사각형의 경우에는 3을 제외한 나머지 숫자들이 이미 쓰여있으므로 가운데 빈 칸에는 3이 들어가야 한다.

이와 같이 빈 칸을 차례로 채워 가면 다음과 같은 최종 결과를 얻을 수 있다.

게임 시작 전 스도쿠 판에 쓰여 있는 숫자들의 정보가 주어질 때 모든 빈 칸이 채워진 최종 모습을 출력하는 프로그램을 작성하시오.
입력
아홉 줄에 걸쳐 한 줄에 9개씩 게임 시작 전 스도쿠판 각 줄에 쓰여 있는 숫자가 한 칸씩 띄워서 차례로 주어진다.
스도쿠 판의 빈 칸의 경우에는 0이 주어진다. 스도쿠 판을 규칙대로 채울 수 없는 경우의 입력은 주어지지 않는다.
출력
모든 빈 칸이 채워진 스도쿠 판의 최종 모습을 아홉 줄에 걸쳐 한 줄에 9개씩 한 칸씩 띄워서 출력한다.
스도쿠 판을 채우는 방법이 여럿인 경우는 그 중 하나만을 출력한다.
해설
이 문제도 마찬가지로 백트래킹 알고리즘을 사용해서 풀어야하는 문제이다.
import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.StringTokenizer
import kotlin.system.exitProcess
private lateinit var board: Array<Array<Int>>
private lateinit var zeroPosition: MutableList<Pair<Int, Int>>
fun main() {
val br = BufferedReader(InputStreamReader(System.`in`))
board = Array(9) { Array(9) { 0 } }
zeroPosition = mutableListOf()
repeat(9) { i ->
var st = StringTokenizer(br.readLine())
for (j in board.indices) {
board[i][j] = st.nextToken().toInt()
if (board[i][j] == 0)
zeroPosition.add(Pair(i, j))
}
}
back(0)
}
private fun back(depth: Int) {
if (depth == zeroPosition.size) {
for (i in board.indices) {
for (j in board.indices) {
print("${board[i][j]} ")
}
println()
}
exitProcess(0)
}
val x = zeroPosition[depth].first
val y = zeroPosition[depth].second
for (i in 1 until 10) {
if (check(x, y, i)) {
board[x][y] = i
back(depth + 1)
board[x][y] = 0
}
}
}
private fun check(x: Int, y: Int, value: Int): Boolean {
var checkValue = value
for (i in board.indices) {
if (i == y)
continue
if (board[x][i] == checkValue)
return false
}
for (i in board.indices) {
if (i == x)
continue
if (board[i][y] == checkValue)
return false
}
var startX = (x / 3) * 3
var startY = (y / 3) * 3
for (i in 0..2) {
for (j in 0..2) {
if (i == x && j == y)
continue
if (board[startX + i][startY + j] == checkValue)
return false
}
}
return true
}
배열 자체가 9 x 9의 크기로 고정되어 있기에 무조건 브루트포스 알고리즘으로 해결이 가능할 것 같아 브루트포스알고리즘을 이용했다.
우선 모든 경우의 수를 확인하기전 최대한 시간복잡도를 줄이기 위하여 입력받는 배열에서
0의 위치를 기억하는 배열인 private lateinit var zeroPosition: MutableList<Pair<Int, Int>> 를
만들어 주었다.
private fun back(depth: Int) {
if (depth == zeroPosition.size) {
for (i in board.indices) {
for (j in board.indices) {
print("${board[i][j]} ")
}
println()
}
exitProcess(0)
}
val x = zeroPosition[depth].first
val y = zeroPosition[depth].second
for (i in 1 until 10) {
if (check(x, y, i)) {
board[x][y] = i
back(depth + 1)
board[x][y] = 0
}
}
}
백트래킹 알고리즘 사용한 코드인데 이는 N과 M 시리즈 처럼
- 상태를 변경하는
board[x][y] = i - 재귀하는
back(depth + 1) - 다시 상태를 원래대로 되돌리는
board[x][y] = 0부분으로 구성되어 있다.
다만 여기서 check(x, y, i) 라는 함수를 사용했는데 이는 (x, y) 위치에 i라는 값이 들어올 수 있는지 2차원 배열을 탐색하면서
스도쿠의 규칙에 어긋나지 않으면 true, 어긋나면 false 를 return하는 함수이다.
마지막으로 depth == zeroPosition.size 을 통하여 return 규칙을 만들어 주었고, 스도쿠의 답이 여러개 나올 수도 있지만
한개의 스도쿠 답만 출력하는 문제였기에 exitProcess(0) 을 통하여 현재의 프로세스를 종료해주었다.

하지만 여기서 시간이 496ms가 걸린 것을 확인할 수 있었는데 이는 비교적 느린편에 속하였다.
최근에 알고리즘을 풀더라도 최대한 시간을 줄이는 방식으로 최적화하는 연습을 진행중이었기에
나름 최적화를 하기 위해 노력했지만 실력이 부족하여 400대 중반까지밖에 줄이지 못하였다.
다른 사람의 코드를 확인하였는데 다른사람들은 정말 대단한 것 같다…
우선 코드부터 보여주겠다.
import java.io.BufferedReader
import java.io.InputStreamReader
import java.lang.StringBuilder
import java.util.StringTokenizer
import kotlin.system.exitProcess
private lateinit var board: Array<Array<Int>>
private lateinit var zeroPosition: MutableList<Pair<Int, Int>>
private var row = Array(10){ BooleanArray(10) { false } }
private var col = Array(10){ BooleanArray(10) { false } }
private var block = Array(10){ BooleanArray(10) { false } }
fun main() {
val br = BufferedReader(InputStreamReader(System.`in`))
board = Array(9) { Array(9) { 0 } }
zeroPosition = mutableListOf()
repeat(9) { i ->
var st = StringTokenizer(br.readLine())
for (j in board.indices) {
board[i][j] = st.nextToken().toInt()
if (board[i][j] == 0)
zeroPosition.add(Pair(i, j))
else{
row[i][board[i][j]] = true
col[j][board[i][j]] = true
block[3 * (i / 3) + j / 3][board[i][j]] = true
}
}
}
back(0)
br.close()
}
private fun back(depth: Int) {
if (depth == zeroPosition.size) {
var sb = StringBuilder()
for (i in board.indices) {
for (j in board.indices) {
sb.append(board[i][j]).append(" ")
}
sb.append("\n")
}
println(sb)
exitProcess(0)
}
val (x, y) = zeroPosition[depth]
val b = 3 * (x / 3) + y / 3
for (i in 1 until 10) {
if(!row[x][i] && !col[y][i] && !block[b][i]){
row[x][i] = true
col[y][i] = true
block[b][i] = true
board[x][y] = i
back(depth + 1)
board[x][y] = 0
row[x][i] = false
col[y][i] = false
block[b][i] = false
}
}
}
여기서 내 코드와의 차이점은 나는 check라는 함수를 사용하였기에 규칙에 만족하는지 확인하는 시간복잡도가 O(n)이 걸렸을테지만
위의 코드에서는 별도의 배열을 통해서 확인하기에 시간복잡도가 O(1)가 걸려 훨씬 빠른 코드가 된 것이다.
여기서 배열은 총 3개를 사용하였는데
- 열을 확인하는
row배열 - 행을 확인하는
col배열 - 3 x 3에서 숫자가 단 하나만 존재하는지 확인하는
block배열이다.
block 배열에서는 특이하게 block[3 * (i / 3) + j / 3][board[i][j]] 을 사용하여 확인한다.
예를들어 (2, 2)에 위치하는 값은
(0, 0) (0, 1) (0, 2)
(1, 0) (1, 1) (1, 2)
(2, 0) (2, 1) (2, 2)
위 블록에 값과 비교하여 중복된 값이 아닌지 확인한다.
여기서 3 * (i / 3) + j / 3 라는 식을 사용하게되면 위의 있는 좌표들은 전부 0이라는 값을 가지게 되는것이다.
다른 예로 (4, 5)에 위치하는 값은
(3, 3) (3, 4) (3, 5)
(4, 3) (4, 4) (4, 5)
(5, 3) (5, 4) (5, 5)
에 해당하는 블록에서 검사를 진행하는데 3 * (i / 3) + j / 3 이 식을 사용함으로써 전부 4 라는 값을 가지게 되는 것이다.
그렇게해서
for (i in 1 until 10) {
if(!row[x][i] && !col[y][i] && !block[b][i]){
row[x][i] = true
col[y][i] = true
block[b][i] = true
board[x][y] = i
back(depth + 1)
board[x][y] = 0
row[x][i] = false
col[y][i] = false
block[b][i] = false
}
}
부분에서 단지 block[b][i] 즉, b라는 블록안에 i라는 값을 true로 만들어주기만 하면
나중에 규칙검사하는데 단 한번의 연산으로 확인할 수 있게 되는 것이다.

이렇게 하게되면 496ms라는 시간에서 240ms 약 2배정도 빠른 시간에 코드가 실행된 것이다.
'안찌의 개발일기 > Algorithm' 카테고리의 다른 글
| 백준 1068 - 트리(Kotlin) (1) | 2023.11.27 |
|---|---|
| 백준 2661 - 좋은 수열 (코틀린) (0) | 2023.11.22 |
| 백준 15649 N과 M (코틀린) (0) | 2023.10.16 |
| 백준 9663 N-Quuen(코틀린) (0) | 2023.10.16 |
| [백준 5904] Moo 게임 (Kotlin) (1) | 2023.10.11 |